Человечество становится всё изобретательнее

Распространение незнания об окружающем
мире тоже должно быть научно подкреплено. 
Ежи Лец

Рисунок скопирован с сайта www.newscientist.com

 

В 2004 году довольно много шума среди обывателей наделала статья американского физика Хьюбнера ¹. В этой статье Хьюбнер предложил некий показатель изобретательности человечества – норму изобретательства. Он определил норму как количество научных открытий и технических изобретений за год, деленное на численность населения. Назовём показатель Хьюбнера H-нормой, тогда

H(t)= Q(t)/P(t), (1)

где

H(t) - H-норма в году t;

Q(t) - количество научных открытий и технических изобретений за год t; плотность их во времени;

P(t) - численность населения в году t.

H-норму можно подсчитывать для отдельной страны или для мира в целом.

Хьюбнер считал, что H-норма есть изобретательность среднего человека. Всеобщее мнение неявно сводится к тому, что изобретательность среднего человека должна оставаться почти постоянной на протяжении веков, т. е. количество изобретений всегда прямо пропорционально численности населения. Однако по расчетам Хьюбнера, функция H(t) не постоянна. До середины XIX века H-норма росла, а затем начала уменьшаться, т. е. график H-нормы имеет колоколообразный вид. Хьюбнер предсказывал, что к 2050 году H-норма упадет до уровня средних веков, т. е. средний человек середины XXI века будет не более изобретателен, чем человек времен инквизиции. По оценке Хьюбнера, данной в 2004 году, человечество вплотную приблизилось к пределу изобретательности, после которого его изобретательность начнет падать.

После 2004 года прошло уже шесть лет, и можно уточнить эту оценку, воспользовавшись свежими статистическими данными об изобретательстве и о численности населения. Кроме того, можно сделать некие предположения об изобретательности некоторых наций.

Патентная статистика

Как справедливо отметил Хьюбнер, количество научных открытий и технических изобретений в последние полтора-два столетия можно оценивать посредством выданных патентов. Несмотря на целый ряд недостатков и ограничений, присущих патентной статистике, вряд ли найдется лучшая количественная мера изобретательности. Патентная статистика по странам, присоединившимся к Гаагской конференции, ведется с 1883, она опубликована Всемирной организацией интеллектуальной собственности WIPO ². Построенный по данным WIPO график количества патентов как функции времени Q(t) показан ниже (Рисунок 1).

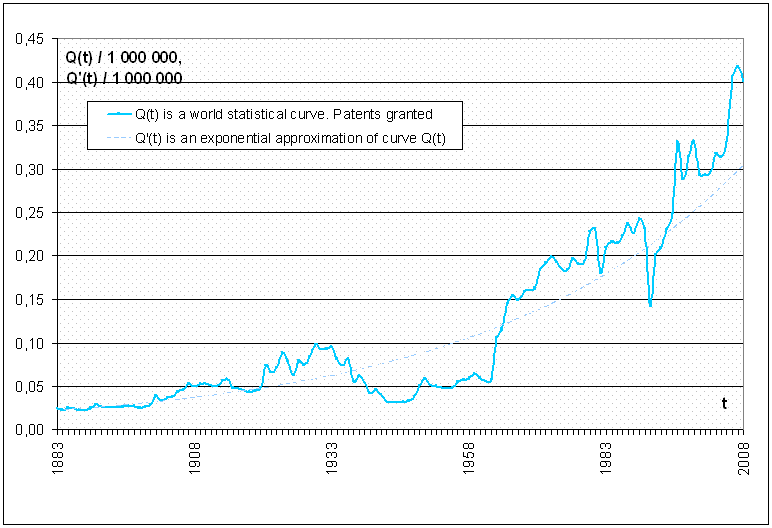
Рисунок 1 – Количество выданных в мире патентов

Суммарное количество патентов Q(t), выданных во всех странах, неуклонно растет, если наблюдать за функцией на отрезках времени с длиной около 50 лет. К примеру, в 1900 году по всему миру было выдано около 28 тысяч патентов, в 1950 – уже почти 59 тысяч, а в 2000 году – 293 тысячи. С другой стороны, некоторые короткие участки функции Q(t) являются провальными, на них функция временно убывает. Провалы в числе выданных патентов легко объясняются двумя мировыми войнами, изменениями в патентном учете, распадом Советского Союза и пр.

В предвоенные и военные годы обеих мировых войн многие страны (Германия, Япония, Великобритания, СССР, Италия) самоизолировались, засекретили свои изобретения, запретили передачу заявок на изобретения в другие страны. Эти действия вызвали общемировые спады патентной регистрации, которые видны на графике Q(t) как два провала: с 1914 по 1921 и с 1933 по 1961 годы.

Провал 1962 года связан, по-видимому, с изменением общемировых правил учета патентов. В этот и предыдущий год многие национальные ведомства не выделяли из общего числа патентов резидентные и нерезидентные заявки, хотя делали так и до, и после 1962 года.

Провал 1991 года связан с распадом Советского Союза и приостановкой регистрации изобретений (но не изобретательства) на его территории. Регистрация в бывших советских республиках возобновилась через несколько лет: в России, Латвии, на Украине в 1992 году, в Белоруссии, Узбекистане   в 1993, в Киргизии   только в 1994. Прежний советский уровень регистрируемого изобретательства восстановился не сразу.

Несмотря на безусловную случайность, стохастичность изобретательского процесса, его аппроксимирующая функция Q’(t) является возрастающей и, по всеобщему мнению, подчиняется экспоненциальному закону.

H-норма за последние двести лет по патентной статистике

Итак, абсолютное количество выданных в мире патентов продолжает расти. А как ведет себя относительная H-норма? Если в последние годы население планеты увеличивается намного быстрее, чем умнеет, то H-норма должна убывать. Проверим, так ли это, по графику H(t) (Рисунок 2). График построен по последним данным о выданных патентах ² и о численности населения Земли ^[3], ⁴.

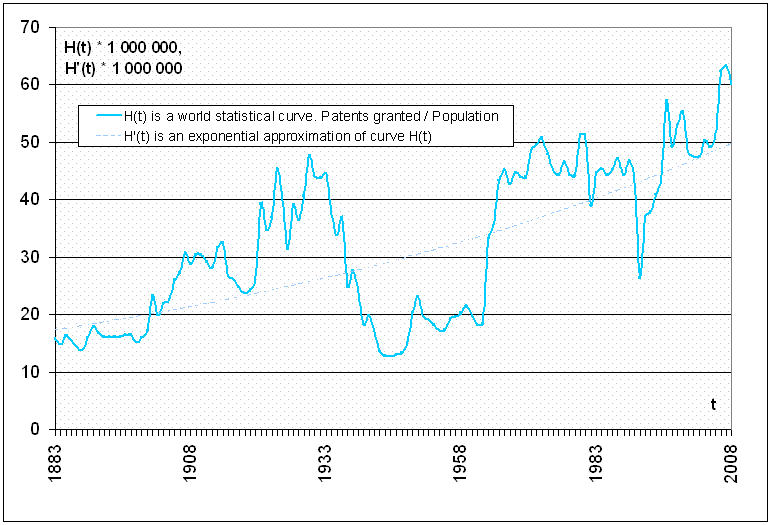
На отрезке от 1883 по1949 год численность населения рассчитана по ³, на отрезке от 1950 по 2008 год численность населения рассчитана по ⁴.

Рисунок 2 – Количество выданных в мире патентов, нормированное к численности населения планеты

На кривой H-нормы есть те же провалы, что и на кривой Q(t) (Рисунок 1). Кривая не выглядит колоколообразной, как это предвещал Хьюбнер, и её аппроксимирующая функция является возрастающей. К примеру, в 1900 году на каждый миллион населения Земли приходилось 17 патентов, в 1950 – 23 патента, а в 2000 – уже 48 патентов. Это означает, что «средний человек» за сто лет «поумнел» почти в три раза. Рост изобретательности продолжается и в последнее десятилетие. За десять лет с 1998 по 2008 год изобретательность выросла с 53 до 60 патентов на миллион населения планеты.

Поскольку ООН отмечает снижение скорости роста населения Земли и прогнозирует дальнейшее снижение прироста вплоть до 2050 года ⁴, то от H-нормы можно ждать даже ускорения в росте, так как знаменатель в дроби (1) растет медленнее, чем числитель. Следовательно, прогноз Хьюбнера о снижении H-нормы не оправдался, и нет никаких предпосылок к его проявлению.

Интересно было бы также взглянуть назад не на двести лет, а в более отдаленное прошлое, в Средние века, как заглянул туда Хьюбнер. Мы воспользуемся теми же самыми данными, но другим приёмом.

H-норма за последние полтысячи лет

К сожалению, в Средневековье не было патентных бюро, а государи и инквизиция слабо разбирались в статистике. Поэтому надежных статистических сведений об изобретательстве в те столетия у нас нет. Но есть прекрасный сборник «История науки и техники» ⁵ двух авторов, Банча и Хелеманса, на который ссылался Хьюбнер. В сборнике есть сведения от каменного века вплоть до 2003 года. Однако, как уже отмечалось, более объективной за последние сто лет будет патентная статистика.

Разумеется, что на многовековом отдалении от тех событий авторам сборника, как и всем нам, видны лишь самые значимые изобретения. Далеко не все нынешние патенты достойны той же известности, что и упомянутые в сборнике изобретения. Очевидно, что исторические веса рядовых современных патентов и всемирно известных изобретений различны. Тем не менее, можно дать грубую оценку для переводного коэффициента из одного веса в другой, чтобы затем построить кривую важных изобретений. Именно важных. Кривая важных изобретений объединит на общей оси времени известные изобретения прошлого, начиная со Средних веков, и патенты последнего столетия.

Возьмем мирный 1905 год. В большинстве европейских стран и в США патентное дело было уже хорошо налажено. До Первой мировой войны было еще далеко, особого режима секретности не было, изобретения публиковались и патенты выдавались. Согласно ⁵ в 1905 году было 26 событий. В этом же году было выдано 44273 патента. Это означает, что среди всех патентов только один из примерно 1700 достоин упоминания в сборнике Банча и Хелеманса ⁵. Теперь описанным ниже приемом совместим две кривые: патентную кривую и кривую важных изобретений. Из патентной кривой, нарисованной выше (Рисунок 2), высечем участок от 1905 до 2008 года и дополнительно отнормируем функцию на переводной коэффициент важности изобретения, т. е. на 1700. На том же графике на отрезке от 1450 до 1905 года построим по данным ⁵ кривую важных изобретений. Кривые сойдутся в точке 1905 года (Рисунок 3).

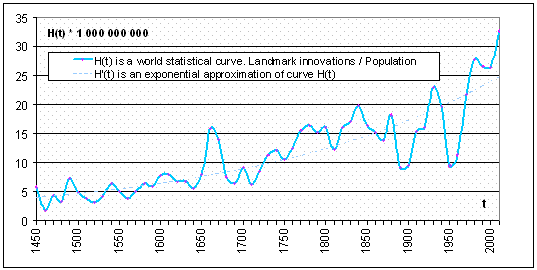
На отрезке с 1450 по 1905 год кривая H(t) построена на данных ⁵, на отрезке с 1906 по 2008 год кривая H(t) построена на данных ², дополнительно отнормированных на коэффициент 1700.

Рисунок 3 – Количество важных изобретений человечества, нормированное к численности населения планеты

На графике не видно никаких проявлений снижения удельной (подушевой) изобретательности у землян за последние 558 лет. H норма не уменьшается. Более того, H норма растет экспоненциально, и её рост продолжается на большом отрезке времени от 1450 до 2008 года. Причем в последние годы с 2000 по 2008 рост является ускоренным.

Чем же подкреплялось беспокойство Хьюбнера по поводу насыщения кривой изобретательности? По всей видимости, опасения Хьюбнера вызваны не общемировыми, а национальными показателями в США.

H-норма по странам

Совершенно другой вид имеют кривые H-нормы, построенные на национальных данных, а не на общемировых. Кривую H-нормы по патентам, выданным в США, Хьюбнер построил в 2004 году. Благодаря последним данным ⁶-⁸ эта кривая удлинилась до 2008 года (Рисунок 4).

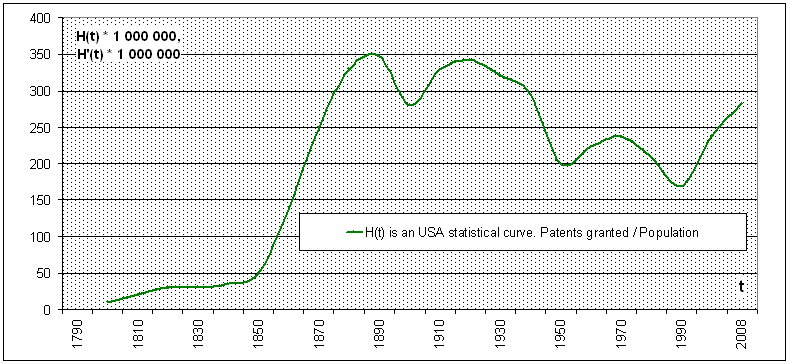
Рисунок 4 – Количество патентов, выданных резидентам в США, нормированное к численности населения страны

Эту кривую – кривую изобретательности в США   нельзя назвать неуклонно возрастающей, но и неуклонно убывающей её тоже не назовешь. Видимо, из-за хода этой кривой у Хьюбнера появились пессимистические сомнения в изобретательских способностях человека.

И напротив, оптимизм появляется, если посмотреть на графики кривых для Японии, Кореи, Китая. Кривая H-нормы для Японии, построенная по патентной статистике ² и численности ⁹, рвется вверх, у кривой нет признаков близкого убывания; аналогичный вид у корейской H нормы (Рисунок 5), график которой построен на данных ² и ¹⁰.

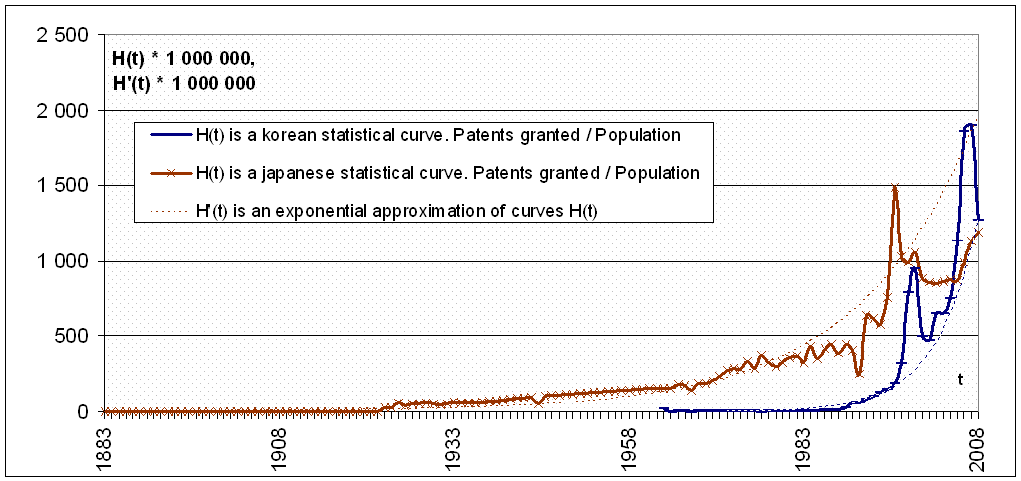
Рисунок 5 – Количество патентов, выданных резидентам в Корее и Японии, нормированное к численности населения страны

Итак, далеко не все кривые национальных H-норм рвутся вверх, а некоторые из них действительно имеют колоколообразный вид. Другими словами, в некоторых странах удельная изобретательность уже была наибольшей и сейчас убывает, а в других странах всё набирает скорость на подъеме. Можно ли найти здесь закономерность? Если народы живут в одну эпоху, то чем вызвано их различное отношение к изобретательству? Объяснение такой национальной характеристике можно найти в теории этногенеза Гумилева ¹¹.

Теория этногенеза

Кратко и упрощенно идеи Гумилева можно изложить так. Этногенез – это появление, развитие, угасание и исчезновение этноса, т. е. народа.

Нет ни одного древнего этноса – из нам известных, – сохранившегося до наших дней в целостном виде. От шумеров, этрусков, римлян, эллинов, финикийцев, майя, египтян, кривичей, персов остались только следы: романтические легенды, великолепные развалины, глиняные таблички, черепки, пирамиды, пергаменты. От этносов, появившихся много раньше, с самого начала развития человеческого вида, не осталось ничего. Этнос появляется в результате генной мутации, изменяющей поведенческий стереотип, который становится пассионарным¹, т. е. страстным, жертвенным. «Пассионарность – стремление действовать без всякой видимой цели или с целью иллюзорной. … Пассионарий не может не действовать» ¹¹.

Этносы появляются, проходят в своем развитии несколько последовательных фаз и исчезают, следовательно, у этносов есть возраст, есть младенчество, рост, зрелость, увядание и старость. Только на фазе зрелости (по Гумилеву: надлом и инерция) этнос перенаправляет энергию своей жертвенности. Этнос перестает самоутверждаться как новый народ и начинает самоутверждаться в искусстве и науке: «при невысокой пассионарности и достаточных способностях люди самоуправляются в областях, не связанных с риском: в искусстве, науке, преподавании и технических изобретениях. В предыдущую фазу они бы с мечами боролись за свои идеалы, а теперь они… ставят эксперименты по теории тяготения, как Ньютон и Галилей…» ¹¹.

Гумилев выдвинул научную концепцию этногенеза, т. е. жизненного цикла народа, продолжающегося около полутора тысяч лет. Гумилев не проводил статистических расчетов по изобретательности древних этносов. Такие расчеты на примерах древних этносов есть в моей предыдущей статье ¹², и эти расчеты подтверждают концепцию Гумилева. Действительно, расцвет наук и техники у древних народов, полный жизненный цикл которых нам уже известен, приходится всего лишь на несколько столетий внутри этногенеза. Кривые абсолютной изобретательности Q(t) для эллинов, римлян, византийцев, арабов-мусульман, славян ¹² отрываются от нуля лишь в «зрелом» этническом возрасте, а вне этого возраста следов изобретательства и творчества почти не обнаруживается. Поэтому кривую этнической изобретательности Q(t), построенную в сильно сглаженном виде и для одного этноса, пережившего и своё младенчество и свою старость, можно считать колоколобразной. Очевидно, что соответствующие нормированные этнические кривые H(t) тоже будут колоколобразными.

К примеру, кривая H-нормы для римского этногенеза без сильного сглаживания на участке от зарождения римлян до их исчезновения выглядит как кочка (Рисунок 6). Эта кривая построена на данных по изобретательности римлян ¹² и по их численности ¹³ и ¹⁴.

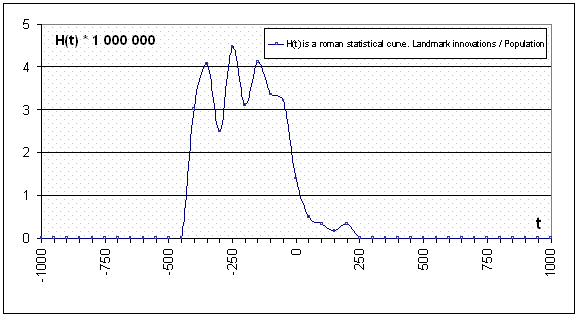
Рисунок 6 – Количество важных изобретений древних римлян, нормированное к их численности

Пик изобретательности древних римлян пришелся на 250 год до н. э., в то время как пик этногенеза – на четырехсотые-пятисотые годы до н. э. Другими словами, этническая изобретательность прирастает, когда этногенез уже прошел свой максимум. У этноса-младенца и у этноса-старца этническая изобретательность равна нулю. Следовательно, сильно сглаженная кривая этнической изобретательности похожа на колокол. Римская кривая идеально иллюстрирует связь этнической изобретательности и этногенеза.

Заключение

Удельная (на душу населения) изобретательность всего человечества ускоренно растет. Нет никаких проявлений или предпосылок к её скорому снижению. Статистическая функция удельной изобретательности аппроксимируется экспонентой.

Сильно сглаженная и усредненная кривая удельной изобретательности отдельного этноса (народа) имеет колоколообразный вид, если наблюдать за кривой на протяжении 1,5-2 тысяч лет. Поскольку существование этноса почти всегда ограничено во времени и вне временных границ своего существования этнос не способен к изобретательству, то левый и правый хвосты кривой лежат на оси абсцисс. Пик изобретательства проявляется у этноса на фазе спада этногенеза, на фазе спада жизненного цикла. Следовательно, по форме этнических кривых изобретательности Q(t) или H(t) можно судить о текущей фазе этногенеза у живого этноса.