Монитор комплексов заданий в ОС ЕС

Стандартные средства языка управления заданиями ОС ЕС ЭВМ требуют постоянного участия оператора в процессе счёта сложных программ, что вызывает дополнительные временные затраты, увеличивает расход ресурсов и является основным источником ошибок, особенно при выполнении комплексов, содержащих большое количество взаимосвязанных заданий. В последнее время  появился ряд программных средств [1-4], позволяющих автоматизировать обработку комплексов заданий.

Наиболее развитое прикладное средство [1] организует выполнение “технологических цепочек’’, составленных из заданий, и модифицирует тексты заданий. Основными недостатками этой системы являются последовательное выполнение заданий внутри технологических цепочек, отсутствие связи между последними, “безусловное” выполнение заданий и наличие ограничения на их количество в одной цепочке (10-15), а также замещение фрагментов текста JCL вручную, а не по алгоритму модификации.

Управление сетью заданий в SVS 7.1 [4] предоставляет широкие возможности, но не позволяет модифицировать задания, что необходимо при наличии больших баз данных, требующих регулярного выполнения процедур обеспечения их целостности и эффективности.

Предлагаемая мониторная программа обладает значительно более гибким, чем в [1] , входным языком, не накладывает ограничений на технологию счета, на количество контролируемых заданий, их имена, имена наборов данных и томов внешней памяти. Язык позволяет описать схему выполнения заданий с указанием условий вида “ЕСЛИ задание завершилось аварийно, ТО….”. Аппарат замещения текста заданий полностью автоматизирован.

Будем описывать комплексы взаимосвязанных заданий на языке гиперграфов, который позволяет компактно отображать сложные структуры и характер связи между их элементами [5].

Условия взаимосвязи заданий естественным образом представляются ребрами ориентированного гиперграфа, множество вершин которого совпадает с множеством заданий комплекса.

На рис. 1,а изображен фрагмент, представляющий условие “задания B, C и D выполняются после окончания задания A”, на рис. 1,б – фрагмент, представляющий условие “задание D выполняется после завершения заданий A, B и С”. Очевидно, входимость ребра в вершину определяет конъюнкцию элементарных условий типа “задание завершено”, а условие запуска задания есть дизъюнкция входящих конъюнкций (рис. 1,в).

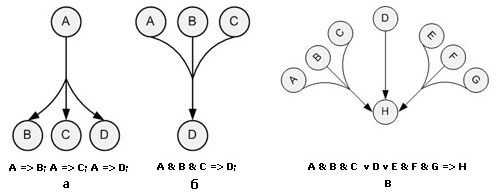
Рис. 1. Примеры взаимосвязи заданий

Все множество условий определяет связанный ориентированный гиперграф комплекса заданий. Требуется различать нормальное и аварийное завершение заданий, поэтому введем раскраску рёбер, а алгоритм выполнения всего комплекса будем соотносить с алгоритмом раскраски вершин гиперграфа.

Итак, в начале работы все вершины окрашены в цвет V, ребра, соответствующие нормальному завершению, - в цвет n, а аварийному – в цвет e. Запущенное задание соответствует вершине цвета S, задание, завершившееся нормально, - вершине цвета N, аварийно – цвета E .

Вершины гиперграфа раскрашиваются по следующим правилам:

1. В цвет S перекрашиваются V-вершины, если они не имеют входящих рёбер.

2. S-вершины перекрашиваются в цвета E и N в зависимости от характера завершения задания.

3. Вершина раскрашивается в цвет S , если выполнена хотя бы одна из конъюнкций, определяемая входящим в вершину ребром, причем конъюнкция, связанная с ребром, считается выполненной, если это:

- n-ребро и все его истоки суть N-вершины;

- e-ребро и все его истоки суть E-вершины.

Для безусловного выполнения пункта 1 можно ввести фиктивную N-вершину.

Нетрудно убедиться в том, что все возможные системы условий запуска заданий, зависящих от характера окончания предыдущих, адекватно представимы таким гиперграфом, а процесс выполнения комплекса взаимосвязанных заданий моделируется процессом раскраски по приведенным правилам.

Анализ реальных комплексов показал, что можно ограничить полустепень исхода для всех вершин числом 2 (по одному ребру каждого цвета), кроме того, достаточно ограничиться ребрами с одним истоком, как на рис. 1,а или с одним стоком, как на рис. 1,б.

С этими ограничениями, практически не влияющими на изобразительные возможности, гиперграфовую модель можно использовать для управления счетом. При этом алгоритм счёта интерпретируется как алгоритм раскраски.

Не будем рисовать e – ребро, если оно-петля (это соответствует возможности повторять задание после его аварийного завершения без предварительных восстановительных действий). Тогда изображение узлов с одним стоком и с одним истоком на алфавитно-цифровом дисплее, пригодное для их обработки на ЭВМ, может быть, например, таким, как на рис. 2 и 3 соответственно.

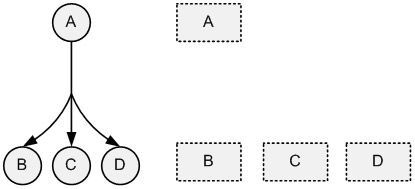
Рис. 2. Представление ребра гиперграфа с одним истоком на алфавитно-цифровом дисплее

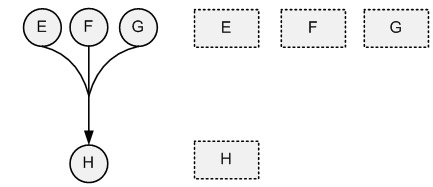
Рис. 3. Представление ребра гиперграфа с одним стоком на алфавитно-цифровом дисплее

Ребра цвета e будем показывать как на рис. 4. С помощью этих фрагментов (см. рис. 2-4) можно описать любой гиперграф, подчиняющийся перечисленным ограничениям.

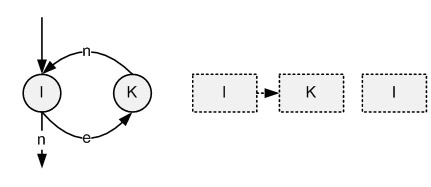
Рис. 4. Представление ребра гиперграфа, соответсвующего аварийному завершению задания, на алфавитно-цифровом дисплее

Для компактного изображения больших гиперграфов введем понятие блока, соответствующее понятию подграфа.

Блок – это набор строк, которые выполняются последовательно, т. е. одна за другой. Строка содержит от нуля до четырех вершин, выполняемых параллельно, или один оператор аварии. Каждая вершина может быть или именем задания, оформленного по правилам ОС, или именем другого блока. Оператор аварии предписывает специальные действия в случае аварийного завершения указанного в нем задания: 1 – выполнение некой вершины и повторение аварийного задания или 2 – приостановка выполнения комплекса. В блоке могут быть, кроме того, резервные, служебные строки и строки-комментарии.

Каждую вершину в блоке снабдим двумя индикаторами, первый из которых отмечает её цвет (V – исходное состояние – пробелом; S – начало выполнения – знаком “?”; N – нормальное завершение – знаком “+”; E – аварийное завершение – знаком “-”), а второй содержит признак вершины (пробел – задание; M – модифицируемое задание; Б – блок).

Модификация текстов заданий производится по шаблонному принципу по собственным алгоритмам модификации. Данные об алгоритмах, шаблонах и модификаторах, относящиеся к заданиям, хранятся в отдельном наборе данных.

Монитор вызывается в последнем шаге каждого задания сети, он же и дополняет вновь формируемые задания шагом для вызова самого себя. Такая организация снимает проблему фрагментации и простоя памяти и психологический барьер “еще одного монитора”.

Описанная мониторная система позволяет значительно упростить работу оператора ЭВМ, исключить технологические ошибки и автоматизировать модификацию текста заданий. Она “прозрачна” для оператора и пользователя, не требует изменений в заданиях и обеспечивает простой переход из программного режима контроля в операторский. Опыт применения монитора показал его высокую надежность, простоту и эффективность. По предварительной оценке реальное время выполнения сложных комплексов заданий сокращается в среднем на 20%.

Список литературы

1. Еремин Г. С. Мониторная система для пакетной  обработки заданий в ОС ЕС // Программирование. 1986. № 6. с. 48-56.

2. Егоров И. В. , Музычкин П. А. Автоматизация процесса пакетной обработки заданий в ДОС ЕС ЭВМ // Там же. 1982. № 1.  с. 62-65.

3. Степаненко А. Г. Система управления решением сетевых задач в вычислительной сети ЕС ЭВМ // Управляющие системы и машины. 1987. № 3. с. 42-47.

4. Единая система электронных вычислительных машин. Операционная система ОС 7.1.  Язык управления заданиями. 05116-0301-1 E 0051. Дрезден: VEB ROBOTRON, 1985.

5. Берштейн П. С., Малышев Н. Г. Применение гиперграфов для представления сложных систем // Изв. АН СССР. Сер. «Техническая кибернетика». 1975. №5. с. 68-73.