Об оценке малых вероятностей при помощи обобщенного распределения экстремальных значений
УДК 621.391.2
Автореферат
В кратком сообщении предлагается алгоритм определения параметров обобщенного распределения экстремальных значений, с помощью которого можно оценить пороговый уровень при заданной вероятности ложной тревоги. Эта задача часто возникает при моделировании радиотехнических систем на ЭВМ.
Один из параметров распределения оценивается методом моментов, два других - методом максимального правдоподобия. Применение этого алгоритма позволяет в несколько раз уменьшить объем испытаний по сравнению с прочими известными алгоритмами. Приводятся сравнительные характеристики погрешности предлагаемого и одного из известных алгоритмов.
Краткое сообщение
1. При моделировании радиотехнических систем на ЭВМ часто возникает необходимость по небольшому числу испытаний оценить вероятность появления редкого события, например, ложной тревоги. Применение в этих случаях специальных статистических методов обеспечивает значительный выигрыш в числе испытаний по сравнению с непосредственной оценкой [1].
Пусть случайная величина X имеет плотность вероятностей f(x) и распределение F(x), тогда для оценки вероятности p(x0)=1-F(x0) превышения порога x0 объем испытаний должен быть порядка 10/p(x0)[1]. Объем испытаний можно уменьшить на порядок, если использовать для оценки p(x0) асимптотическое распределение экстремальных значений, и на два порядка при использовании обобщенного (трехпараметрического) распределения, предложенного в [2]. Оба метода основаны на разбиении выборки на группы по n элементов в каждой группе и последующему поиску экстремума в группе. При p(x0) ≤ 102 и распределении F(x) экспоненциального типа оценка p(x0) [2] имеет вид:
(1) ![]()
2. Метод оценки параметров ![]() , описанный в [3], в практических приложениях дает значительную погрешность по следующим причинам:
, описанный в [3], в практических приложениях дает значительную погрешность по следующим причинам:
а) процедура определения оценки ![]() как производной от функции
как производной от функции ![]() по двум точкам n1,n2 весьма груба и чувствительна к способу разбиения исходной выборки на группы, из которых извлекаются экстремумы;
по двум точкам n1,n2 весьма груба и чувствительна к способу разбиения исходной выборки на группы, из которых извлекаются экстремумы;
б) последующее применение метода максимального правдоподобия (ММП) к отысканию оценки dn позволяет определить точку максимального правдоподобия в сечении, определяемом положением ![]() , далеком от истинного значения экстремума.
, далеком от истинного значения экстремума.
Для устранения отмеченных недостатков целесообразно применить ММП. Однако, ввиду овражного характера функции правдоподобия, применение стандартных (градиентных) методов поиска экстремума оказывается неэффективным. Поэтому в приведенном ниже алгоритме предлагается определять ММП два параметра ![]() и dn, оценивая характеристический экстремум un методом моментов [4], поскольку, как показали результаты моделирования, погрешность такой оценки
и dn, оценивая характеристический экстремум un методом моментов [4], поскольку, как показали результаты моделирования, погрешность такой оценки ![]() составляет несколько процентов.
составляет несколько процентов.
Предлагаемый алгоритм основан на комбинации метода «золотого сечения» [5] и метода Ньютона для решения нелинейного уравнения (см. приложение). При необходимости возможно дальнейшее уточнение оценок градиентными методами по всем трем параметрам.
3. Для сравнения эффективности предлагаемого метода и метода, предложенного в [3], проводилось вероятностное моделирование на ЭВМ. Параметры ![]() вычислялись по выборке объема k=4000 при различных разбиениях выборки на группы. По полученным оценкам с помощью (1) определялся пороговый уровень
вычислялись по выборке объема k=4000 при различных разбиениях выборки на группы. По полученным оценкам с помощью (1) определялся пороговый уровень ![]() для заданной вероятности p(x0). Усредненное по 30 экспериментам значение
для заданной вероятности p(x0). Усредненное по 30 экспериментам значение ![]() сравнивалось с точным значением порога, определяемым по уравнению
сравнивалось с точным значением порога, определяемым по уравнению ![]() . Точность оценивалась относительной погрешностью
. Точность оценивалась относительной погрешностью ![]() и относительным стандартным отклонением
и относительным стандартным отклонением ![]() . Результаты моделирования для нормального распределения представлены на рис. 1.
. Результаты моделирования для нормального распределения представлены на рис. 1.
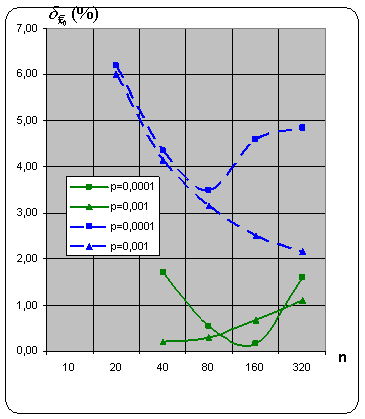
Рис. 1. Относительная погрешность ![]() оценки порогового уровня в зависимости от размера n группы для двух алгоритмов. Штриховая линия - алгоритм из [3], сплошная линия - предлагаемый алгоритм.
оценки порогового уровня в зависимости от размера n группы для двух алгоритмов. Штриховая линия - алгоритм из [3], сплошная линия - предлагаемый алгоритм.
Предлагаемый метод дает заметно меньшую погрешность в определении порога по сравнению с методом [3] и, кроме того, обладает меньшей чувствительностью к разбиению выборки на группы. Несмотря на большую сложность предложенного метода, затраты машинного времени на его реализацию по сравнению с [3] возросли незначительно: при объеме контрольной выборки k = 104 оно составило 40 с на ЭВМ ЕС-1022.
Алгоритм оценивания параметров
А. Предварительный этап
1. Выборку ![]() разбить на N групп по n элементов в каждой (k=N*n) и выбрать максимальные значения
разбить на N групп по n элементов в каждой (k=N*n) и выбрать максимальные значения ![]() в каждой группе.
в каждой группе.
2. Определить оценки параметров ![]() ,
, ![]() методом моментов [4]:
методом моментов [4]:
![]() ,
, ![]() ,
, 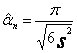 ,
, ![]() ,
, ![]() (постоянная Эйлера).
(постоянная Эйлера).
3. Выбрать границы возможного изменения параметра ![]() (для широкого класса распределений 1 ≤
(для широкого класса распределений 1 ≤ ![]() ≤ 2); обозначить левую и правую границы
≤ 2); обозначить левую и правую границы ![]() 1,
1, ![]() 4; вычислить промежуточные точки методом «золотого сечения»:
4; вычислить промежуточные точки методом «золотого сечения»:
![]() ,
, ![]() ,
, ![]() .
.
4. В каждой из точек ![]() найти ММП оценку параметра
найти ММП оценку параметра ![]() . В качестве начального приближения выбрать
. В качестве начального приближения выбрать ![]() , уточнение осуществить методом Ньютона для уравнения
, уточнение осуществить методом Ньютона для уравнения
![]() , где
, где ![]()
(Решение уравнения определяется с точностью до 0,1 % за 1-2 итерации).
5. В найденной таким образом точке ( ![]() ,
, ![]() ,
, ![]() ) вычислить значение логарифма функции правдоподобия
) вычислить значение логарифма функции правдоподобия
![]()
B. Итерационный цикл
1. Сузить интервал изменения 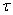 , отбросив отрезок [τ1, τ2] в случае W2 < W3 или отрезок [τ3, τ4] в случае W2 ≥ W3.
, отбросив отрезок [τ1, τ2] в случае W2 < W3 или отрезок [τ3, τ4] в случае W2 ≥ W3.
Произвести необходимую пересылку.
2. Провести одно дополнительное сечение (п. А3) по параметру 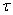 в новых границах.
в новых границах.
3. Выполнить пп. А4, А5 для нового сечения.
4. Повторить итерационный цикл, пока не будет выполнено условие |τ1 - τ4| < l, где l - наперед заданная константа порядка 0,1.
5. При выходе из цикла точка максимума функции правдоподобия будет находиться внутри прямоугольника:
(τ1, ![]() ) (τ1,
) (τ1, ![]() ) (τ4,
) (τ4, ![]() ) (τ4,
) (τ4, ![]() )
)
Литература
- Экстремальные статистики и машинное моделирование в применении к системам с кодово-импульсной модуляцией. E. Biglierri и др. - Экспресс-информация, серия «Радиолокация, телевидение, радиосвязь, № 30, 1971, стр. 14-35.
- Weinstein S. Теория и применение некоторых классических и обобщенных асимптотических распределений экстремальных значений. - IEEE Trans IT-19, № 2, стр. 148.
- Филимонов В. А. Оценка малых вероятностей при помощи обобщенного распределения экстремальных значений. - Радиотехника и электроника, 1978, № 2, том XXIII, стр. 451-454.
- Гумбель Э. Экстремальные статистики. - М.: Мир, 1965.
- Батищев Д. И. Поисковые методы оптимального проектирования. - М.: Сов. радио, 1975, стр. 54-56.